Table of contents
Introduction
- In general, the ratio of a number x to a number y is defined as the quotient of the numbers x and y.
- Ratios can be expressed as percentages. To express the value of a ratio as a percentage, we multiply the ratio by 100.
Thus, 4/5 = 0.8 = 80%
Some Important Properties
- If we multiply the numerator and the denominator of a ratio by the same number, the ratio remains unchanged.
That is, a/b = ma/mb - If we divide the numerator and the denominator of a ratio by the same number, the ratio remains unchanged. Thus,
a/b= (a/m)/(b/m) - Denominator equation method: The magnitudes of two ratios can be compared by equating the denominators of the two ratios and then checking for the value of the numerator.
- eg. Which is larger: 8/3 or 11/4
- If either or both the terms of a ratio are a surd quantity, then the ratio will never evolve into integral numbers unless the surd quantities are equal. use this principle to spot options in questions having surds.
- If a/b = c/d = e/f = g/h = k then
K = (a+c+e+g) / (b + d + f + h)
Mathematical use of ratio and Proportions
- As a bridge between 3 or more quantities:
If A: B and B:C is given A:C can be found out - Ratio as a Multiplier
If A: B is 3:1, then the value of B has to be multiplied by 3 to get the value of A.
Calculations
Calculation methods for Ratio comparisons
The Cross Multiplication Method
Two ratios can be compared using the cross-multiplication method as follows:
- Suppose you have to compare 12/17 with 15/19. Then, to test which ratio is higher, cross multiply and compare 12 * 19 and 15 * 17.
If 12 * 19 is bigger the Ratio 12/17 will be bigger. If 15 * 17 is higher, the ratio 15/19 will be higher.
In this case, 15 * 17 being higher, the Ratio 15/19 is higher.
Proportions
When two ratios are equal, then the quantities composing them are said to be proportional. Thus, if a/b = c/d, then a, b, c, d is proportional. This is expressed as
a: b: c: d or a: b = c: d
Variations
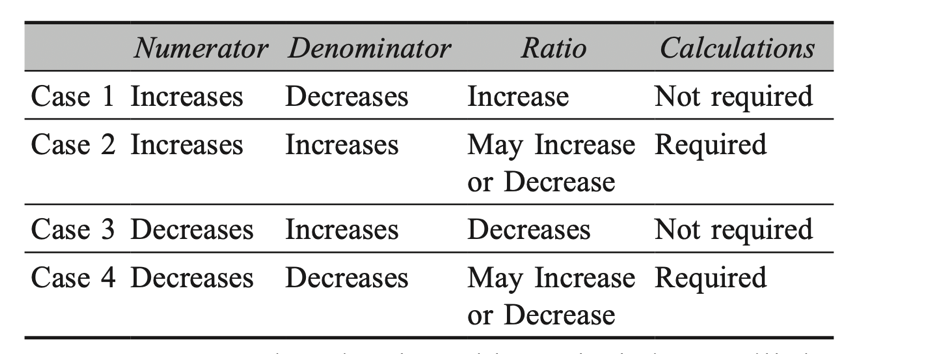
- Direct Proportion (A∝ B)
When it is said that A varies directly as B, you should understand the following implications: - Logical implication: When A increases B increases
- Calculation implication: If A increases by 10%, B will also increase by 10%
- Graphical implications: See following graph
- Equation implication: The ratio A/B is constant
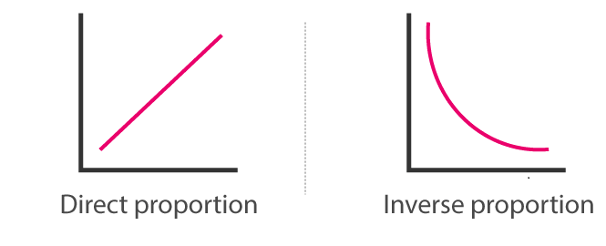
- Inverse Proportion (A∝1/B):
When A varies inversely as B, the following implication arises:
a. Logical implication: When A increases B decreases
b. Calculation implication: If A decreases by 9.09%, B will increase by 10%.
c. Graphical implications: see graph above
d. Equation implication: The product A * B is constant.
Practice Questions:
1. Rs. 5783 is divided among Aman, Balan, and Chintan in such a way that if Rs. 28, Rs. 37 and Rs. 18 are deducted from their respective shares, they have money in the ratio 4:6:9. Find Aman’s share.
a.1228
b. 1245.5
c. 1328
d. 1356
2. If 10 persons can clean 10 floors by 10 mops in 10 days, in how many days can 8 persons clean 8 floors by 8 mops
a. 12 days
b. 10 days
c. 11 days
d. 8 days
3. Rs. 3650 is divided among 4 engineers, 3 MBAs and 5 CAs such that 3 CAs get as much as 2 MBAs and 3 Engineers as much as 2 CAs. Find the share of an MBA.
a. 300
b. 450
c. 475
d. None of these
4. Divide Rs. 1400 into three parts in such a way that half of the first part, one-fourth of the second part and one-eighth of the third part are equal.
a. 300, 600, 500
b. 200, 400, 800
c.100, 400, 1000
d. None of these
5. The ratio of water and milk in a 30-litre mixture is 7: 3. Find the quantity of water to be added to the mixture in order to make this ratio 6:1
a. 30
b. 32
c. 33
d. 35
6. A student appeared in 6 papers. The maximum marks are the same for each paper. His marks in these papers are in the proportion of 5: 6: 7: 8: 9: 10. overall he scored 60%. In how many numbers of papers did he score less than 60% of the maximum marks? (UPSC 2021)
a. 2
b. 3
c. 4
d. 5
7. Out of 120 applications for a post, 70 are males and 80 have a driver license. What is the ratio of between the minimum to maximum number of males having driver's license.
(UPSC 2013)
a.1:2
b.2:3
c.3:7
d.5:7
8. In a rare coin collection, there is one gold coin for every three non-gold coins. 10 more gold coins are added to the collection and the ratio of gold coins to non-gold coins would be 1 : 2. Based on the information; the total number of coins in the collection now becomes.
(UPSC 2013)
a. 90
b. 80
c. 60
d. 50
9. The ratio of a two-digit natural number to a number formed by reversing its digits is 4:7. The number of such pairs is (UPSC 2019)
a. 5
b. 4
c. 3
d. 2
10. The monthly incomes of X and Y are in the ratio of 4 : 3 and their monthly expenses are in the ratio of 3: 2. However, each saves Rs. 6,000 per month. What is their total monthly income?
(UPSC 2017)
a. 28,000
b. 42,000
c. 56,000
d. 84,000
11. The monthly incomes of Peter and Paul are in the ratio of 4:3. Their expenses are in the ratio of 3:2. If each saves Rs. 6,000 at the end of the month, their monthly incomes respectively are (in Rs.) (UPSC 2015)
a. 24,000 and 18,000
b. 28000 and 21000
c. 32,000 and 24,000
d. 34,000 and 26,000
12. A sum of Rs. 2,500 is distributed among X, Y and Z in two ratio 1/2 ∶ 3/4 ∶ 5/6. What is the difference between the maximum share and the minimum share? (UPSC 2020)
a. Rs 300
b. Rs. 350
c. Rs. 400
d. Rs. 450
13. A 6 student appeared in 6 papers. The maximum marks are the same for each paper. His marks in these are in the proportion of 5:6:7: 8:9:10 overall he scored 60%. In how many numbers of papers did he score less than 60% of the maximum marks?
(UPSC 2021)
a. 2
b. 3
c. 4
d. 5
14. Seats for Mathematics, Physics and Biology in a school are in the ratio 5 : 7 : 8. There is a proposal to increase these seats by 40%, 50% and 75% respectively. What will be the ratio of increased seats?
a. 2 : 3 : 4
b. 6 : 7 : 8
c. 6 : 8 : 9
d. None of these
15. The ratio of the number of boys and girls in a college is 7: 8. If the percentage increase in the number of boys and girls be 20% and 10% respectively, what will be the new ratio?
a. 8: 9
b. 17: 18
c. 21: 22
d. Cannot be determined
16. If x varies as y, and y = 4 when x =12, find x when y = 15.
a. 45
b. 54
c. 70
d. 15
17. The ratio of water and milk in a 30-litre mixture is 7:3. Find the quantity of water to be added to the mixture in order to make this ratio 6:1.
a. 6
b. 4
c. 5
d. 7
18. Rahul has coins of the denomination of ₹ 1, 50 p and 25 p in the ratio of 12:10:7. The total worth of the coins he has is ₹ 112.5. Find the number of 25 p coins that Rahul has
a. 48
b. 72
c. 60
d. 42
19. Four numbers in the ratio 1:2:4:8 add up to give a sum of 120. Find the value of the biggest number.
a. 40
b. 30
c. 64
d. 60
20. The ratio between two numbers is 7:11 and their LCM is 154. The first number is:
a. 14
b. 7
c. 22
d. 32
21. A fort has provisions for 60 days. If after 15 days 500 men strengthen them and the food lasts 40 days longer, how many men are there in the fort?
a. 3500
b. 4000
c. 6000
d. None of these
22. The ratio of the age of a man and his wife is 4 : 3. After 4 years, this ratio will be 9 : 7. If at the time of the marriage, the ratio was 5:3, then how many years ago they were married?
a. 8 years
b. 12 years
c. 10 years
d. 15 years
23. 60 litres of diesel is required to travel 600 km using a 800 cc engine. If the volume of diesel required to cover a distance varies directly as the capacity of the engine, then how many litres of diesel is required to travel 800 km using 1200 cc engine?
a. 80 litres
b. 90 litres
c. 120 litres
d. 170 litres
24. If 20 men or 24 women or 40 boys can do a task in 12 days working for 8 hours a day, how many men working with 6 women and 2 boys take to do a task four times as big working for 5 hours a day for 12 days?
a. 8 men
b. 2 men
c. 122 men
d. 24 men
25. If ₹ 232 is divided among 150 children such that each girl and each boy gets ₹1 and ₹2 respectively. Then hoe many girls are there?
a. 52
b. 54
c. 68
d. 62
Log-in to access answers for Ratio, Proportion and Variation and other topics!
If you have made it so far, well done. You are ahead of the competition.
Best of luck!